在网上看到这样一道数学题,是八年级上学期的期末考试填空题。如下:
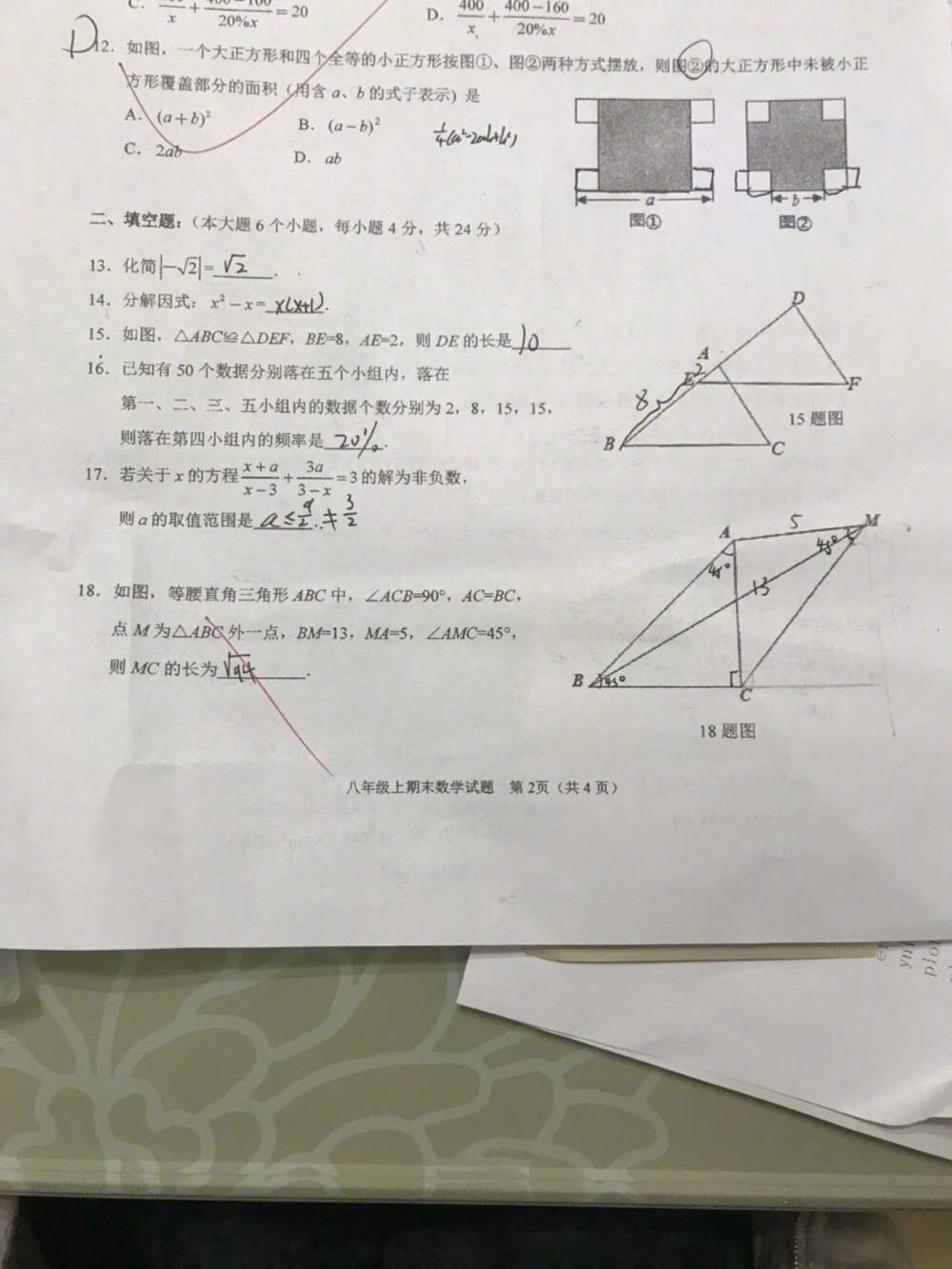
思路:
添加辅助线,利用全等三角形,勾股定理来将已知条件转化为可资利用的数据。
解题图示:
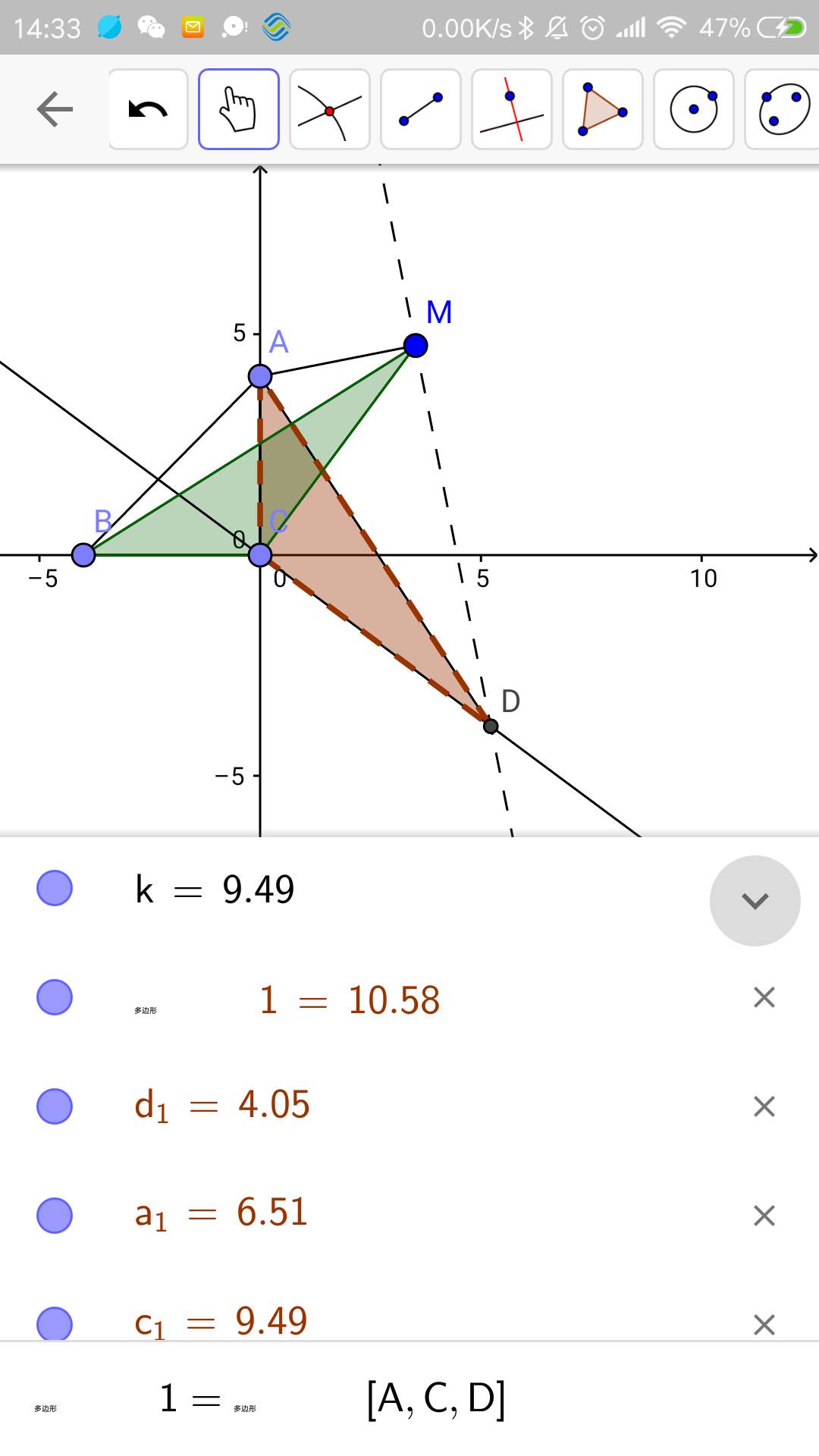
解题过程:
- 过M点作$$\overline{AM}$$的垂线
- 过C点作$$\overline{CM}$$的垂线
- 两线相交于D点。
$$\because \angle AMC=45°$$
$$\therefore \angle CMD=45°$$
$$\therefore$$直角三角形$$\triangle
MCD$$为等腰直角三角形
$$\therefore
\overline{MC}=\overline{CD}$$
又$$\because
\overline{AC}=\overline{BC}$$,$$\angle
BCM=90°+\angle
ACM$$,$$\angle
ACD=\angle
ACM+\angle MCD=\angle
ACM+90°$$
$$\therefore \angle
BCM=\angle ACD$$
$$\therefore
\triangle BCM\triangleq
\triangle ACD$$
两个三角形全等
$$\therefore
\overline{AD}=13$$
$$\because
\triangle
AMD$$是直角三角形,根据勾股定理知
$$\overline{MD}=12$$
又$$\triangle
MCD$$是等腰直角三角形,根据勾股
定理,得
$$\overline{CM}=12\times\sqrt{2}\div2=6\sqrt{2}$$